What is the Byzantine Generals Problem in Distributed Systems?
Understanding How Byzantine Nodes Behave in Distributed Systems
The Byzantine Generals Problem is a thought experiment in distributed computing to understand the challenges of reaching a consensus when some nodes may be untrustworthy or unreliable (node behavior). It shows how difficult it can be to coordinate actions when some system members may act dishonestly.
The Byzantine Generals Problem
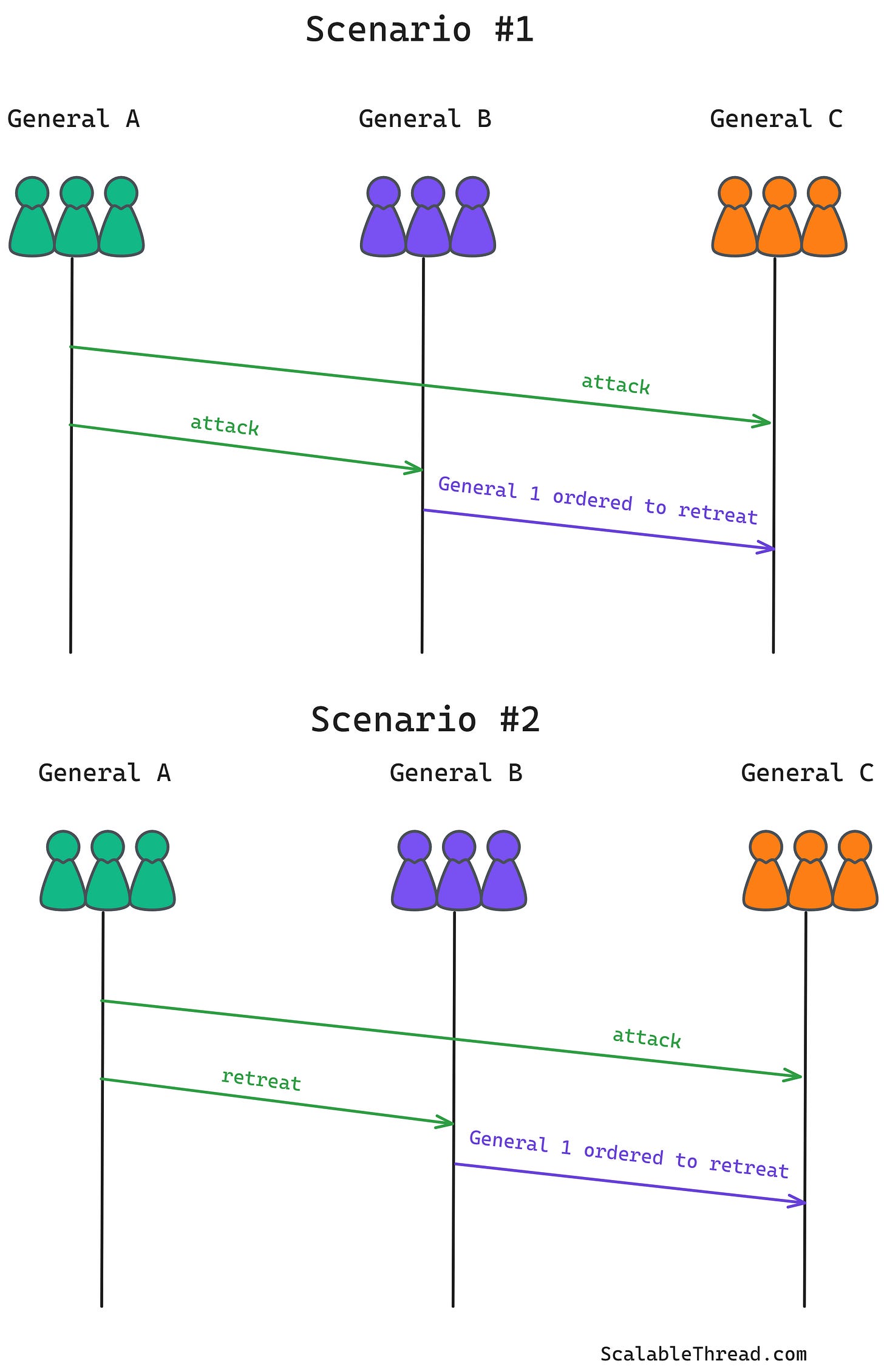
Imagine three or more generals surrounding a city they want to capture. They need to agree on one action: attack or retreat. They can only communicate through messengers. Unlike the two generals problem, the messages will be delivered correctly this time. However, one or more generals could be "traitors" who send false or confusing messages. The honest generals cannot ignore a suspected traitor's message because they don't know who the traitors are. The goal is for all honest generals to agree on the same plan: attack or retreat. For example, if General C receives two contradicting messages—one from General A saying to attack and another from General B saying General A ordered a retreat—General C cannot tell if General B is lying or if General A is giving false information.
Node Behavior in Distributed Systems
In distributed systems, Generals represent the nodes or processes involved. Messages are the communications that happen between these nodes. Traitors are faulty or malicious nodes, known as Byzantine nodes, that may send incorrect or false information. Consensus is the agreement that all working nodes must reach a single value or action (an agreement).
A Byzantine node can behave in unpredictable ways. It might send different messages to different nodes, fake messages, or fail to send messages altogether. This is similar to a general who spreads lies and tries to mess up communication. For example, in a blockchain network, nodes must agree on the order of transactions. A malicious node might try to spread false transactions or mess with the consensus process, risking the integrity of the blockchain.
3f + 1 Rule
The Byzantine Generals Problem has an important limitation: it is impossible to reach an agreement if more than one-third of the participants are faulty. This is the "3f+1" rule, where 'f' is the number of faulty nodes. In simpler terms, if there are 'f' faulty nodes, there must be at least 2f + 1 loyal nodes. This way, even if the faulty nodes team up to share wrong information, the loyal nodes will still have a majority and can reach an agreement.
For example, if we expect at most one faulty node (f=1), we need at least four nodes (3*1 + 1 = 4) in the system. With four nodes, even if one is faulty, the remaining three loyal nodes can vote against the faulty one and reach a consensus.
References
Martin Kleppmann. (2020, October 28). Distributed Systems 2.2: The Byzantine generals problem [Video]. YouTube. https://www.youtube.com/watch?v=LoGx_ldRBU0
If you enjoyed this article, please hit the ❤️ like button.
If you think someone else will benefit from this, then please 🔁 share this post.