Why "What Happened First?" Is One of the Hardest Questions in Large-Scale Systems
Understanding Why Exact Ordering of Events is Hard in Distributed Systems
The Problem with Time
Imagine you and your friend are in different cities. You both look at your watches and agree to clap at exactly 1:00 PM. You clap, but did you both clap at the exact same instant? Probably not. Your watch might be a few seconds faster than your friend's, or maybe it runs a tiny bit slower.
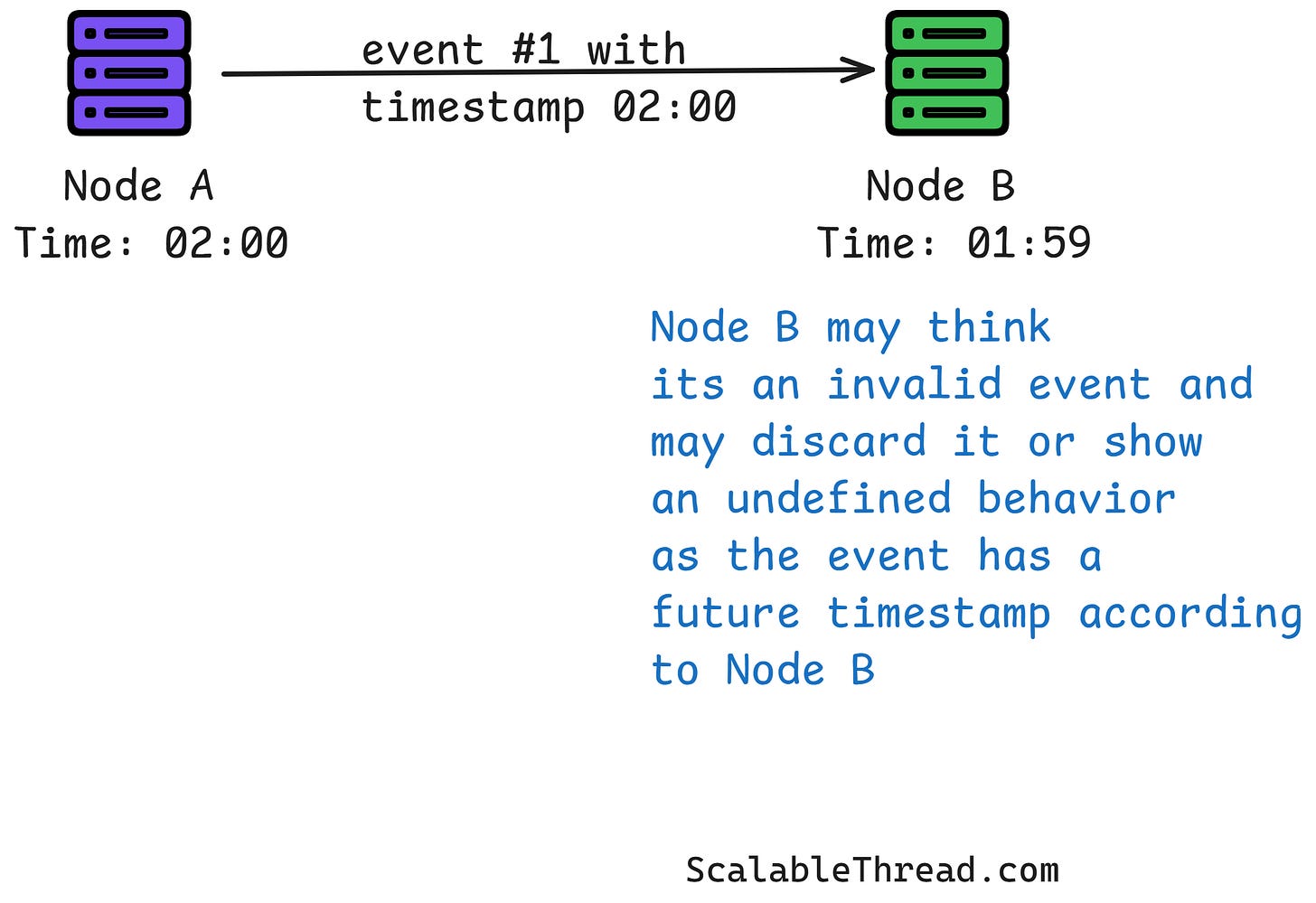
Computers in a large system face the same problem, but on a massive scale. A system like FAANG’s runs on thousands of computers spread across the globe. Each computer has its own internal clock, just like you have your own watch. These clocks are never perfectly in sync.
This creates a big problem: if two events happen on two different computers, it's hard to say with 100% certainty which one happened first just by looking at their timestamps.
Why Clock Synchronization is Hard
The obvious solution seems to be to just synchronize all the computer clocks. We have protocols like the Network Time Protocol (NTP) that try to do this by connecting to ultra-precise atomic clocks. However, even with NTP, achieving perfect synchronization is impossible for two main reasons:
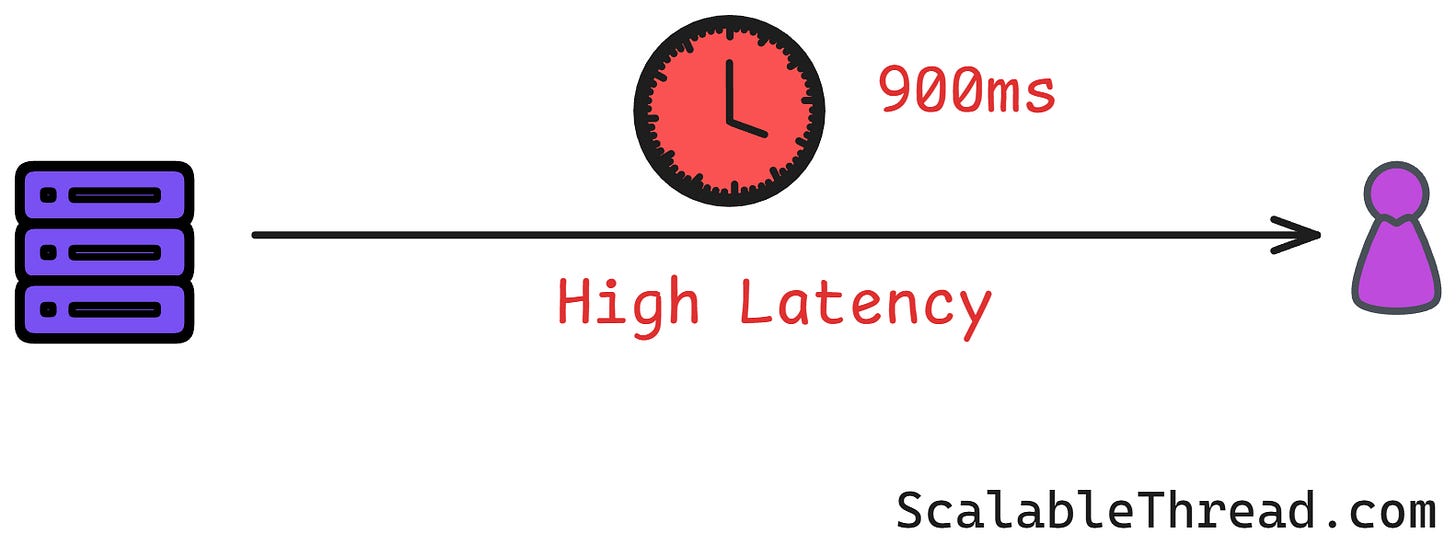
Network Latency: Information doesn't travel instantly. When a computer asks a central time server, "What time is it?", the question takes time to travel to the server, and the answer takes time to travel back. This delay, called latency, is unpredictable. It can change based on network traffic, distance, and other factors. It's like asking your friend for the time over a walkie-talkie with a random delay. You can't be sure if the time you hear is still accurate.
Clock Drift: No two clocks are built exactly the same. The quartz crystals that regulate time in computers vibrate at slightly different frequencies. This causes some clocks to run a little faster and others a little slower. Over time, these small differences add up, and the clocks "drift" apart. Even if you sync them perfectly, they will start to disagree again almost immediately.
Because of these issues, we have to accept that we can never know the exact physical time across a distributed system. The time on one machine might be a few milliseconds ahead of another, and in high-speed large-scale systems, a millisecond is a very long time.
A Workaround: Logical Clocks
If we can't rely on wall-clock time, how do we solve the ordering problem? Computer scientists realized that we don't always need to know the exact time an event happened. Often, it's enough to know the causal order—that is, if one event caused another.
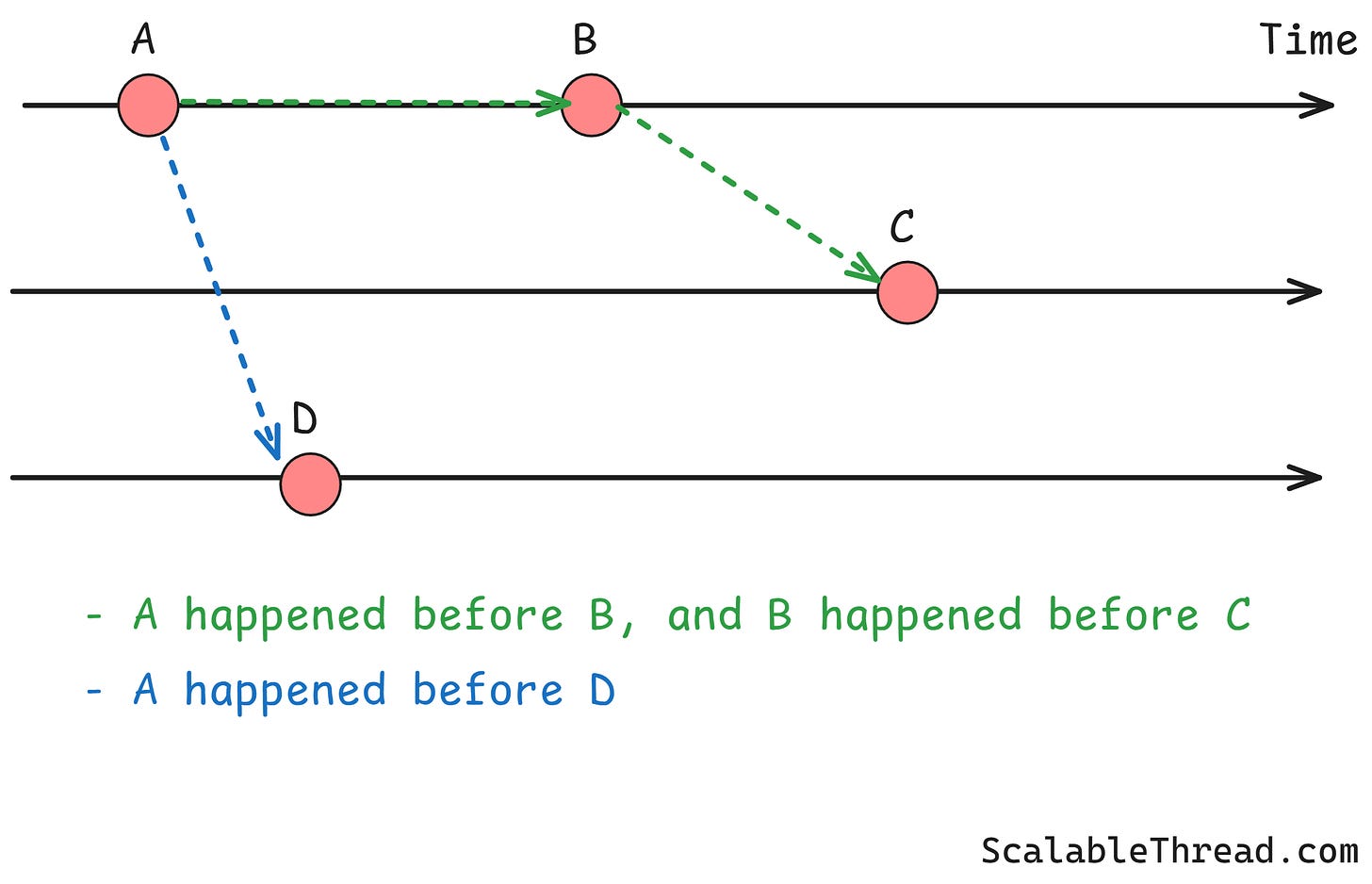
This is called the happened-before relationship. It's simple:
If event A happens on a computer before event B on the same computer, then A happened before B.
If event A is the sending of a message and event D is the receiving of that same message, then A happened before D.
If A happened before B, and B happened before C, then A happened before C.
Events that don't have a happened-before relationship are called concurrent. We can't say which one happened first, and it might not matter. For example, if you send an email to Alice and your friend sends an email to Bob, these events are concurrent.
Logical Clocks
To track this "happened-before" relationship, we can use logical clocks. Imagine each computer in the system has a counter, like a ticket dispenser at a bakery.
Every time an event happens on a computer, it increments its own counter and assigns that number to the event. (e.g.,
counter = counter + 1).When a computer sends a message, it includes its current counter value in the message.
When a computer receives a message, it compares its own counter to the counter in the message. It sets its own counter to the maximum of the two values, and then increments it by one.
An example with two computers, P1 and P2:
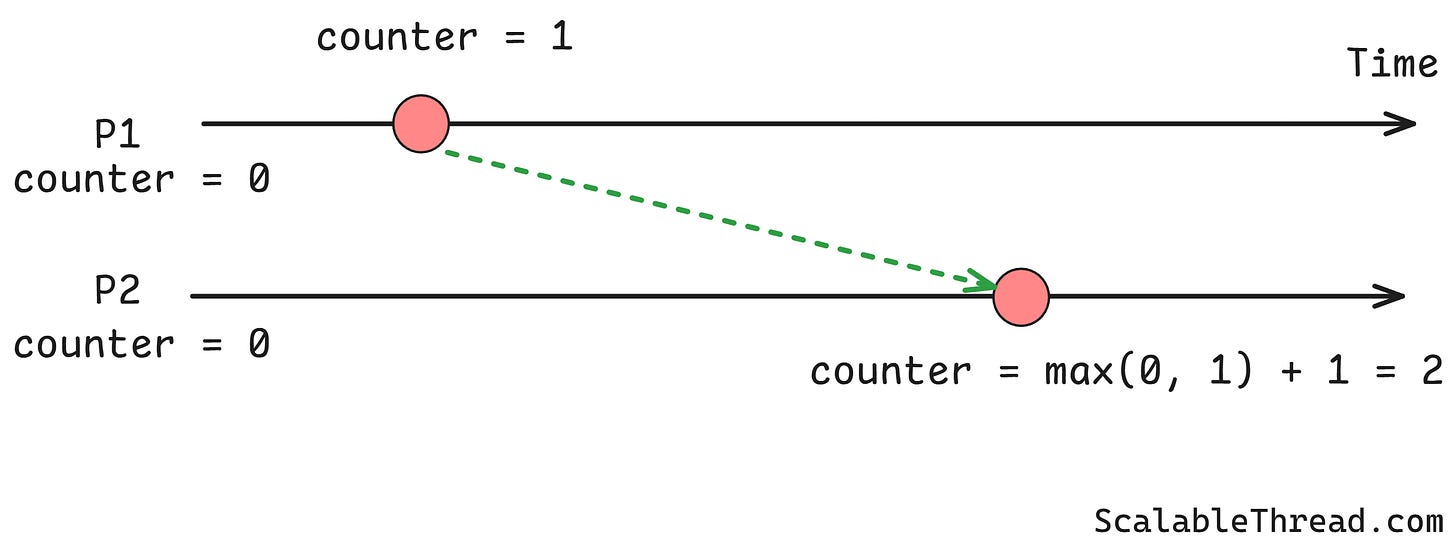
P1 has an internal event. Its counter goes from 0 to 1.
P1 sends a message to P2 with the value 1.
P2 receives the message. Its counter is 0. It sees the message's value is 1. It updates its counter to
max(0, 1) + 1 = 2.P2 has an internal event. Its counter goes from 2 to 3.
By looking at these logical timestamps, we know that the event at P1 (timestamp 1) happened before the event at P2 (timestamp 3). This method guarantees that if event A caused event B, the logical timestamp of A will be less than the timestamp of B.
If you enjoyed this article, please hit the ❤️ like button.
If you think someone else will benefit from this, please 🔁 share this post.

A tough concept explained easily. Pls keep ‘em coming!
Really nice explanation! Glad to find it.